Transformer Meets Boundary Value Problems: Structure-conforming Operator Learning

Abstract

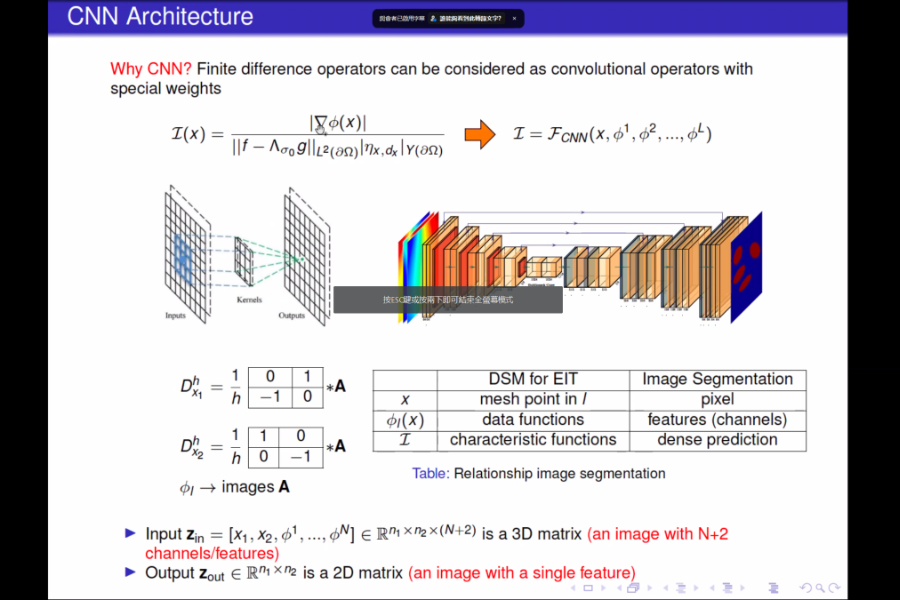
A Transformer-based deep direct sampling method is proposed for solving a class of boundary value inverse problem. A real-time reconstruction is achieved by evaluating the learned inverse operator between carefully designed data and the reconstructed images. An effort is made to give a case study for a fundamental and critical question: whether and how one can benefit from the theoretical structure of a mathematical problem to develop task-oriented and structure-conforming deep neural networks? Inspired by direct sampling methods for inverse problems, the 1D boundary data are preprocessed by a partial differential equation-based feature map to yield 2D harmonic extensions in different frequency input channels. Then, by introducing a learnable non-local kernel, the approximation of direct sampling is recast to a modified attention mechanism. The proposed method is then applied to electrical impedance tomography, a well-known severely ill-posed nonlinear inverse problem. The new method achieves superior accuracy over its predecessors and contemporary operator learners, as well as shows robustness with respect to noise. This research shall strengthen the insights that the attention mechanism, despite being invented for natural language processing tasks, offers great flexibility to be modified in conformity with the a priori mathematical knowledge, which ultimately leads to the design of more physics-compatible neural architectures.

For Attendees' Attention

This talk is hosted by the Department of Mathematics of the Chinese University of Hong Kong and will be held online via Zoom. To attend, please join the Zoom meeting at https://cuhk.zoom.us/j/98241093146 (Meeting ID: 982 4109 3146).

About the Program

For more information, please refer to the program website at https://iasprogram.hkust.edu.hk/inverseproblems/.