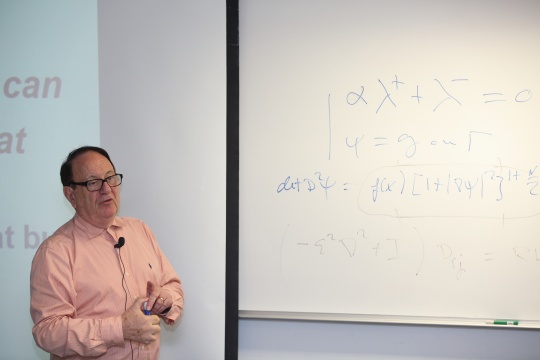The Numerical Solution of the Monge-Ampère Equation

Abstract

The main goal of this lecture is to address the numerical solution of the Dirichlet problem for the elliptic Monge-Ampère equation in dimension two (MA-D). Viscosity methods have been developed for the solution of the (MA-D) if classical solutions do not exist. The problem with viscosity solutions (if classical ones do not exist) is that they verify the Monge-Ampère equation in a bounded convex domain of R-square but violate the boundary condition. Since there are situations (shape design for example) where the boundary condition has to be strictly enforced, we advocate an alternative approach of the (nonlinear) least-squares type.

For the solution of the least-squares formulation, we advocate a (kind of) block-relaxation algorithm. Combined with appropriate finite mixed finite element approximations the above algorithm shows good convergence properties, including those cases where, in the (MA-D), the bounded convex domain of R-square has a curved boundary. Numerical results validating the above methodology will be presented.

About the speaker

Prof. Roland Glowinski received his PhD in Mathematics in 1970 from University of Paris VI, where he had then taught for 15 years before becoming Cullen Professor of Mathematics and Mechanical Engineering at the University of Houston. Recipient of the Seymour Cray Prize, the Grand Prix Marcel Dassault and the SIAM Von Karman Prize, Prof. Glowinski is a member of the French National Academy of Sciences, the French National Academy of Technology and the Academia Europaea. He is also a member of the Morningside Group, with its mission to promote computational and applied mathematics in China.