Norm-dependent Convergence and Stability of the Inverse Scattering Series for Diffuse and Scalar Waves

Abstract

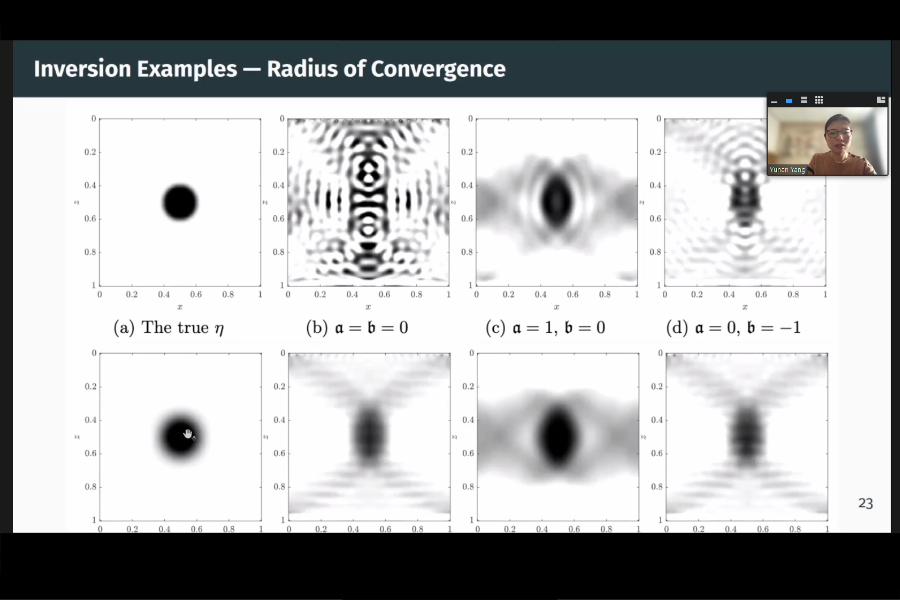
This talk analyzes the forward and inverse scattering series for scalar waves based on the Helmholtz equation and the diffuse waves from the time-independent diffusion equation, which are important PDEs in various applications. Different from previous works, which study the radius of convergence for the forward and inverse scattering series, the stability, and the approximation error of the series under the L^p norms, the speaker and her collaborators study these quantities under the Sobolev H^s norm, which associates with a general class of L^2-based function spaces. The H^s norm has a natural spectral bias based on its definition in the Fourier domain: the case s<0 biases towards the lower frequencies, while the case s>0 biases towards the higher frequencies. They compare the stability estimates using different H^s norms for both the parameter and data domains and provide a theoretical justification for the frequency weighting techniques in practical inversion procedures. They also provide numerical inversion examples to demonstrate the differences in the inverse scattering radius of convergence under different metric spaces.

About the Speaker

Dr. YANG Yunan obtained her BS in Mathematics and Applied Mathematics from Zhejiang University in 2013 and her PhD in Mathematics from the University of Texas at Austin in 2018. In 2018-2021, she was a Courant Instructor in the Courant Institute of Mathematical Sciences at New York University. She then moved to Simons Institute for the Theory of Computing at the University of California, Berkeley as a Simons-Berkeley Research Fellow. In 2022, she joined the ETH Zurich and is currently an Advanced Fellow at the Institute for Theoretical Studies. She will be joining Cornell University as an Assistant Professor of Mathematics in July 2023.

Dr. Yang’s research interests include numerical analysis, computational inverse problems, optimal transport and applications, nonconvex optimization and machine learning. She was awarded the First Prize of the 19^th IMA Leslie Fox Prize for Numerical Analysis by the Institute of Mathematics & its Applications in 2019.

For Attendees' Attention

This talk will be held online via Zoom. To attend, please join the Zoom meeting at https://hkust.zoom.us/j/99768579687 (Meeting ID: 997 6857 9687 / Passcode: iasip2023).

About the Program

For more information, please refer to the program website at https://iasprogram.hkust.edu.hk/inverseproblems/.