Learning Linear Operators from Noisy Data
Abstract
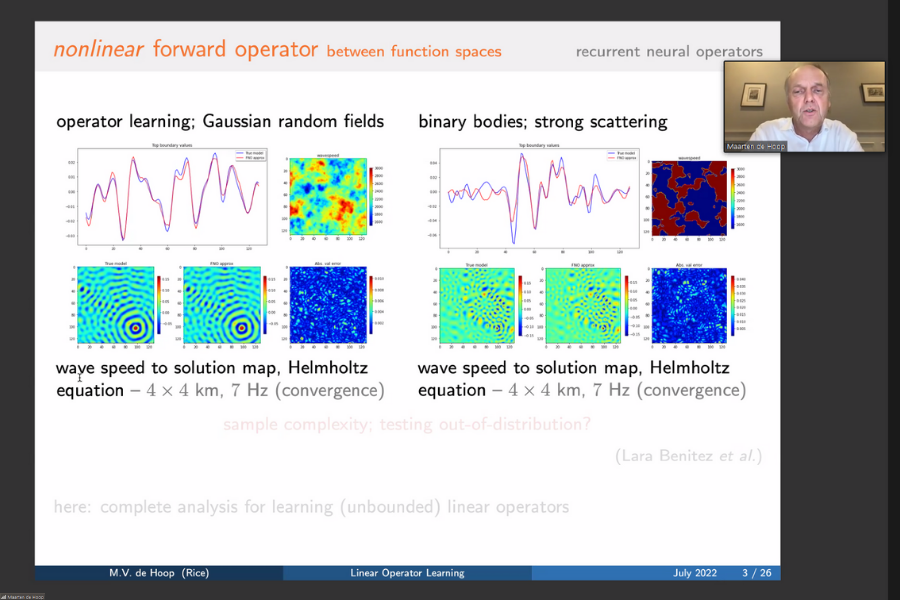
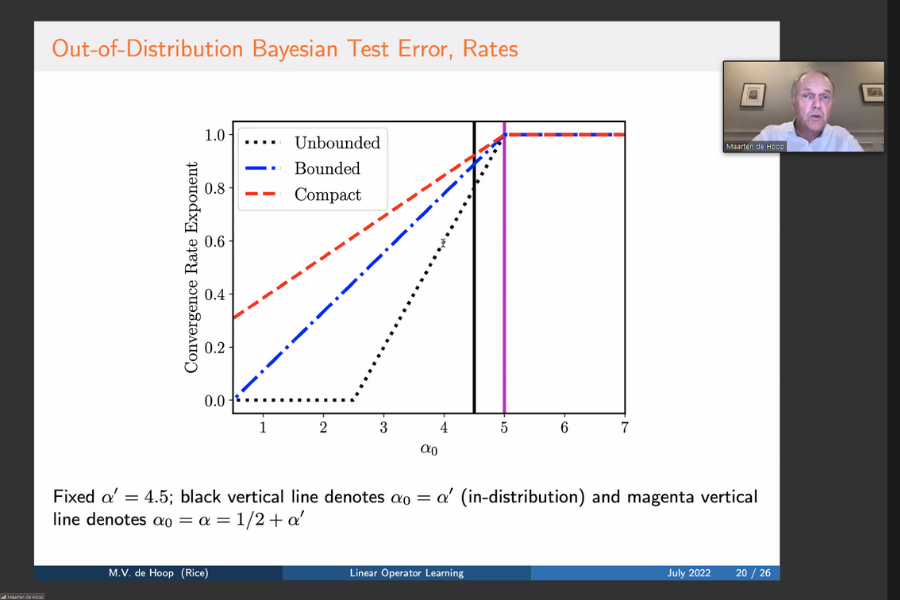
The speaker and his research group study the learning of linear operators between infinite-dimensional Hilbert spaces. The training data comprise pairs of random input vectors in a Hilbert space and their noisy images under an unknown self-adjoint linear operator. Assuming that the operator is diagonalizable in a known basis, this work solves the equivalent inverse problem of estimating the operator’s eigenvalues given the data. Adopting a Bayesian approach, the theoretical analysis establishes posterior contraction rates in the infinite data limit with Gaussian priors. The main results include learning-theoretic generalization error guarantees for a wide range of distribution shifts. These convergence rates quantify the effects of data smoothness and true eigenvalue decay or growth, for compact or unbounded operators, respectively, on sample complexity.
This is a joint research with N.B. Kovachki, N.H. Nelson and A.M. Stuart.
About the speaker
Prof. Maarten V. DE HOOP received his BS in Physics with Mathematics and Astronomy and MS in Theoretical Physics from Utrecht University in 1981 and 1984 respectively. He then obtained his PhD in Technical Sciences from Delft University of Technology in 1992. From 1992 to 1995, he was the Programme Leader and the Senior Research Scientist of Schlumberger Cambridge Research. He joined the Colorado School of Mines (CSM) in 1995 where he was promoted to a Full Professor with the Department of Mathematical and Computer Sciences in 2003. During his tenure at CSM, he was the Co-Leader of the Center for Wave Phenomena. In 2005, he moved to Purdue University as a Professor of Mathematics and of Earth, Atmospheric and Planetary Sciences and became the Director of the Center for Computational and Applied Mathematics. He joined Rice University in 2015 and is currently the Simons Chair in Computational and Applied Mathematics and Earth science.
Prof. De Hoop’s research ranges from the analysis of inverse problems and nonlinear physics to deep learning. He has published more than 180 journal articles, including articles in Science, Nature Communications and Proceedings of the National Academy of Sciences. He also serves on the editorial boards of Inverse Problems, Journal of Inverse and Ill-Posed Problems, and Inverse Problems and Imaging.
Prof. De Hoop is a member of the Society for Industrial and Applied Mathematics, the American Mathematical Society, and the American Geophysical Union. He was elected a Fellow of the Institute of Physics in 2001.
For Attendees' Attention:
This talk will be held online via Zoom. To attend, please join the Zoom meeting at https://hkust.zoom.us/j/95977601102 (Meeting ID: 959 7760 1102 / Passcode: 20220706).
About the program
For more information, please refer to the program website at https://iasprogram.hkust.edu.hk/inverseproblems/.