Inverse Problems for Acoustic Attenuating Media

Abstract

Acoustic attenuation describes the loss of energies of propagating waves. This effect is inherently frequency dependent. Typical attenuation models are derived phenomenologically and experimentally without the use of conservation principles. Because of these general strategies, a zoo of models has been developed over decades.

In this talk, the speaker shall give a (certainly incomplete) survey on attenuation models and will discuss the basic mathematical properties which they have to satisfy in order to be well-posed (in mathematical terms).

Inverse problems, which are considered in this talk, assume attenuation to be known, and consist in determining imaging parameters such as density, absorption, to name but a few, from measurements of waves at the boundary of the object of interest. The speaker and his collaborators will consider two kinds of applications, which are motivated from photoacoustics and ultrasound-tomography.

Photoacoustic imaging is a hybrid imaging technique where the object of interest is excited by a laser and the acoustic response of the medium is measured outside of the object. From this the ability of the medium to convert laser excitation into acoustic waves is computationally reconstructed. For photoacoustics, which is a linear inverse problem, the speaker and his collaborators will determine its spectral values, and they shall see that there are two kinds of attenuating models, resulting in mildly and severely inverse problems.

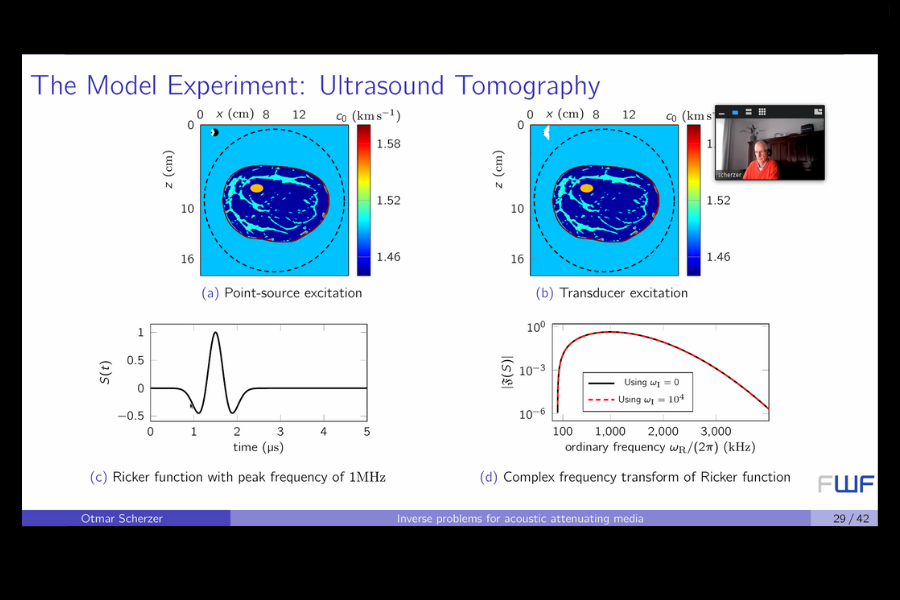
In ultrasound-tomography the object of interest is excited by waves on the boundary and the acoustic response is measured (also at the boundary). The speaker will present an algorithm for the numerical solution of the nonlinear inverse problem and compare the effect of wrongly conjectured attenuation models on the reconstruction.

This is joint work with P. ELBAU, C. SHI (University of Vienna) and Florian FAUCHER (INRIA).

About the Speaker

Prof. Otmar SCHERZER received his MS and PhD, both in Mathematics, from the Johannes Kepler University Linz in 1987 and 1990 respectively. From 1988 to 2000, he held the positions of Assistant Lecturer, Assistant Professor, and Associate Professor at the Johannes Kepler University Linz. He was on the faculty at the Ludwig Maximilian University of Munich (1999-2000), the University of Bayreuth (2000-2001) and the University of Innsbruck (2001-2009). In 2009, he joined the University of Vienna as the Head of Computational Science Center and is currently a Professor for Computational Science at the Department of Mathematics there. He is also the Group Leader of the Inverse Problems and Mathematical Imaging research group at the Johann Radon Institute for Computational and Applied Mathematics of the Austrian Academy of Sciences.

Prof. Scherzer’s research interests are image processing and inverse problems. He has been the Editor-in-Chief of the journal Inverse Problems since 2020. He is also the Associate Editor of Numerical Functional Analysis and Optimization and serves on the editorial board of numerous journals including Journal of Mathematical Imaging and Vision, Journal of Mathematics in Industry and Contemporary Mathematics and Its Applications.

Prof. Scherzer is a Fellow of the Institute of Physics Publishing. In 2018, he was awarded the EAIP award by the Eurasian Association on Inverse Problems. He was also the Vice President of Inverse Problems International Association in 2010-2016.

For Attendees' Attention

This talk will be held online via Zoom. To attend, please join the Zoom meeting at https://hkust.zoom.us/j/93458255506 (Meeting ID: 934 5825 5506 / Passcode: iasip2022).

About the Program

For more information, please refer to the program website at https://iasprogram.hkust.edu.hk/inverseproblems/.